 [Home]
[Home]
Welcome to Fibonacci Mathematics!
You are invited to enter the fascinating world of Fibonacci numbers, the rabbit problem and some more generalizations of the Fibonacci sequence. We will start with a generalization of the rabbit problem. But let us begin with the question :
Who was Fibonacci?
Fibonacci or more correctly Leonardo of Pisa since he was born in Pisa ( Italy ) about 1175 AD and died around 1250 AD was the greatest European mathematician of the middle ages and was one of the first who introduced the Hindu - Arabic number system into Europe, using the arabic symbols 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 and a symbol for zero 0.
Fibonacci wrote 5 mathematical books and in one of them, Liber Abbaci ( 1202) , he introduced a problem to the reader to practise the new mathematics:




The Rabbit Problem
A pair of rabbits are in a field and , if the rabbits take a month to become mature and then produce a new pair every month after that, how many will there be in twelve month time? He assumes the rabbits do not escape and none die. The answer leads to the famous Fibonacci sequence
1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , . . . .
( see on more details also [ 1 ] )
Since then numerous formulae and applications around this sequence have been generated and if you are interested in there exists a wonderful book [ 2 ] .
More about the Fibonacci Sequence!
Are you still interested in? - O.K. You may have again a look at the sequence and wonder how you can obtain the next number of the sequence. You may observe that a number is the sum of the two preceding ones and indeed the sequence follows a so called recurrence formula

So what is needed for the sequence to start with are the first two numbers 1 , 1 . These two numbers are called the seed s ( 0 ) = ( 1 , 1 ).
You may still not be happy since to determine the Fibonacci number for a given value of n you have to work out all the terms which precede it . Fortunately there exist two formulae for this Problem:
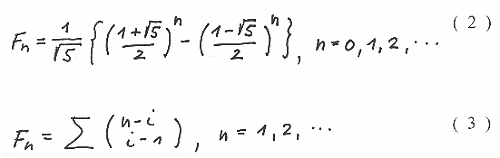
( see also [ 1 ] )