A First Generalization

You may ask what happens with the Fibonacci sequence if the rabbits do not strictly follow human suggestions and become mature say in the k-th month with k = 1 , 2 , . . . and leaving all the other conditions unchanged then we have a first generalization and we ask if there exist a recurrence and a binomial formula equivalent to ( 1 ) and ( 3 ) Here is the answer. With the seed

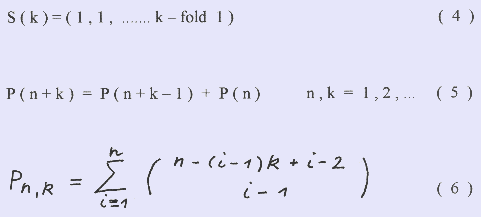
We will first prove the recurrence formula by induction and then show the binomial formula to meet the recurrence formula.

We start with a population P(n) in the n-th month and divide the population into groups of new born rabbits P(1) , one month old ones P(2) and so on up to rabbits k-month old P(k) with P(n) = P(1) + P(2) + ..... + P(k).

We start the induction proof with the verified Fibonacci sequence F(n+2) = F(n+1) + F(n) with F(n) = P(n, k=2) and have a look at Fig.1.

When the rabbit groups start to produce new rabbit pairs, then each group will add every month its start number to the group. So in the (n+k) - th month we have a population P(n+k) = 2 P(1) + 3 P(2) + ..... + (k+1) P(k), which is the sum of P(n+k-1) and P(n). Since in the (n+k+1) month in the P(k) group the first new born rabbits start already again to produce new pairs we get for the total population P(n+k+1) = 3 P + .... + (k+1) P(k+1) + (k+3) P(k), which is the sum of P(n+k) and P(n+1).

Next we will use the binomial theorem and the presentation of its coefficients in the Pascal triangle ( see Fig. 2 ). The sequences have been marked with arrows and the corresponding n-th element a(n) has been assigned in its binomial form ( see Fig. 2 ). Fig. 3 shows the Pascal triangle in its left - justified manner for the Fibonacci sequence each row slipped down two positions against the preceding one

Since A(n) = a(n1) + a(n2) + .....+ a(ni) and n1 = n, n2 = n-2, n3 = n-4, ......, ni = n-2i + 2

We have

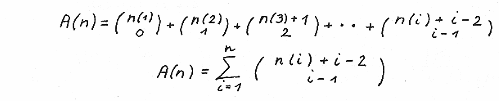
And with ni = n- 2 i + 2

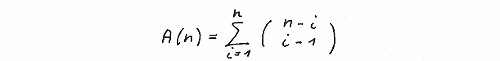
We proof now just for an exercise for the general case that A(n) does fullfill the recurrence equation A(n+2) = A(n+1) +A(n) and therefore A(n) = F(n).

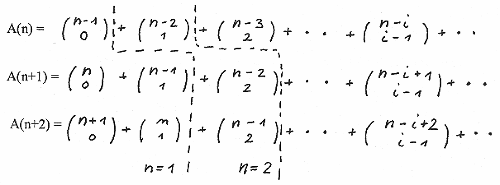
The dotted lines indicate as an example for n=1 and n=2 the limit up to where for a given value of n A(n), A(n+1) and A(n+2) are not zero. So the three equations can be rearranged as follows

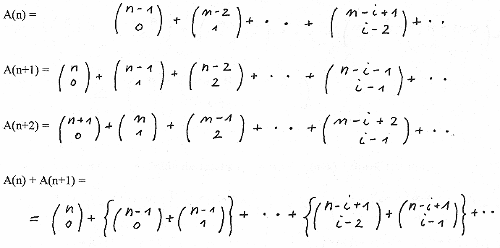
Looking at the i-th element we have

That is A(n) equals F(n).

We show now that in the general case of rabbits pubescent in their k-th month the rows in the Pascal triangle are slipped by k positions against their preceding ones and that the obtained binomial summation formula fullfills the recurrence formula P(n+k) = P(n+k-1) + P(n).

Again B(n) = b(n1) + b(n2) + .... + b(ni) + ...

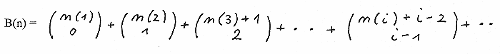
With n1 = n, n2 = n - k, n - 2k, ... , ni = n - (i-1)k, .. i , k = 1 , 2 , .....

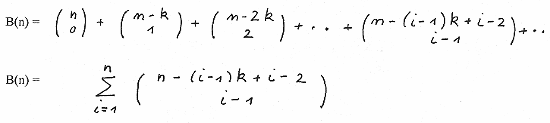
Now we show that that B(n) does fullfill the recurrence equation B(n+k) = B(n+k-1) + B(n).

Again the dotted lines indicate as an example for n=1 and n=2 the limit up to where the B(n), B(n+1) and B(n+2) are not zero. We obtain by rearrangement :

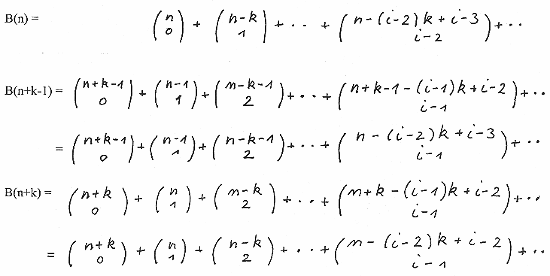
Now looking at the i-th element we have

So B(n+k-1) + B(n) = B(n+k) and B(n+k) = P(n+k).

Below we show examples for k = 1, k = 2, and k = 3 in more detail.

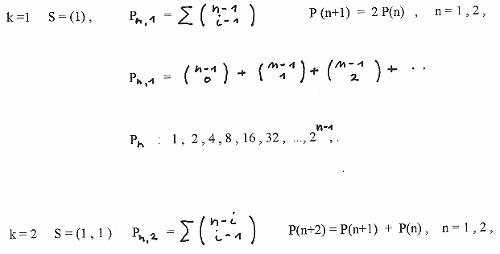
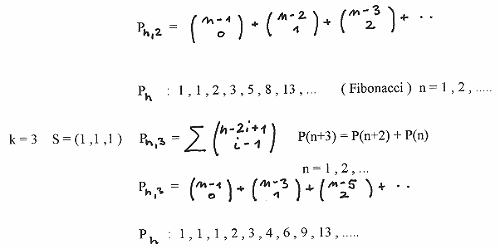
References:

[ 1 ]
R. Knott, Fibonacci Numbers and the Golden Section: http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html

[ 2 ]
S. Vadja, Fibonacci and Lucas Numbers and the Golden Section : Theory and Applications Halsted Press (1989)