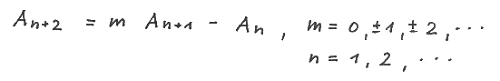A Third Generalization (Part 2)



1.
We start with F (n+2 ) = F (n+1 ) + F (n ) = F (n +1) + F ( n +1) - F (n-1 )
F (n+2 ) = 2 F ( n+1 ) - F ( n-1 )
Observing F ( n-1 ) = F ( n ) - F ( n-2 ) finally yields
F ( n+2 ) = 2 F ( n+1 ) - F ( n ) + F ( n-2 )
The binomial summation formula of the recurrence formula

with seed S ( A (1) , A(2) , A(3) , A(4) ) reads
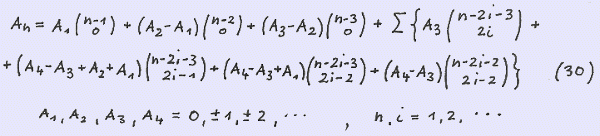
With the seed S ( 1 , 1 , 2 , 3 ) we obtain the Fibonacci sequence and with the seed S ( 1 , 3 , 4 , 7 ) the Lucas sequence respectively :
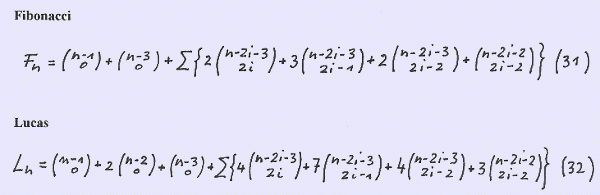
We can rewrite the Fibonacci binomial formula in the more elegant form
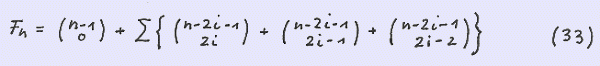
Summing up over n yields
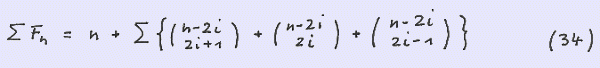
Below we give an example for ∑ F ( n ) of the first nine elements of the sequence.

Replacing n by 2n - 1 and 2n yields F ( 2n-1 ) and F (2n ) respectively:
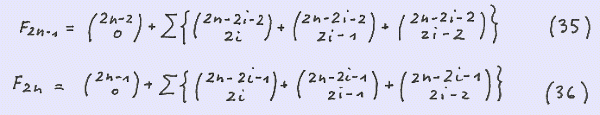
2.
The generalized Fibonacci sequence can be expressed as follows :
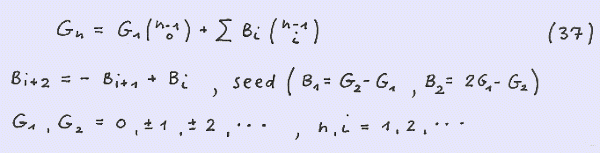
Using the seed S ( 1 , 1 ) and S ( 1 , 3 ) yields the expressions for the Fibonacci and the Lucas sequence respectively :
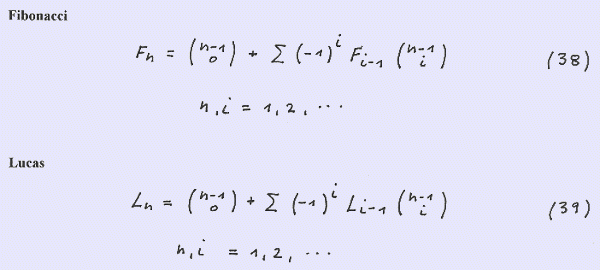
Summing up over n yields the binomial summation formula for ∑ F ( n ) :

As an example again we present the first nine elements of the sequence
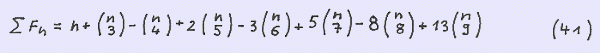
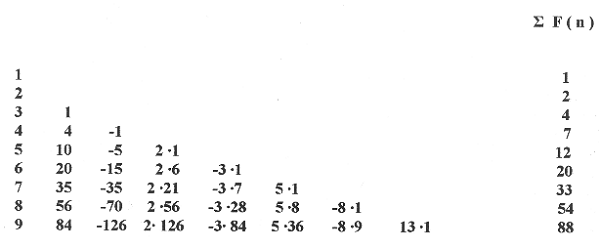
The binomial summation formulae for G ( 2n-1 ) and G ( 2n ) respectively read
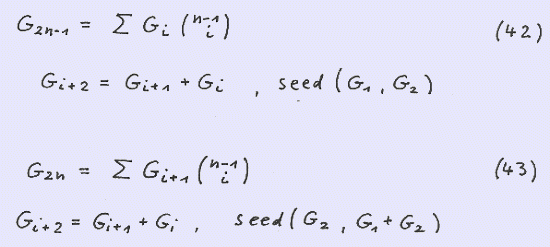
Using the seeds S (1 , 1 ) for the Fibonacci sequence and S ( 1 , 3 ) for the Lucas sequence respectively yields
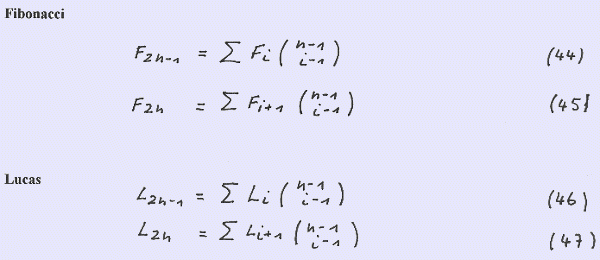
Summing up over n yields
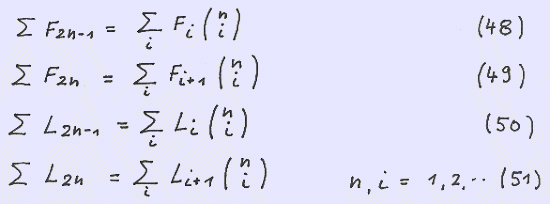
As an example we present the first five elements of the sequence ∑ F ( 2n-1 ) :
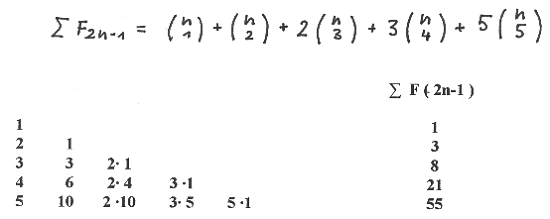
3.
We use here another binomial sum formula for the generalised Fibonacci sequence of every second element G ( 2n-1 ):
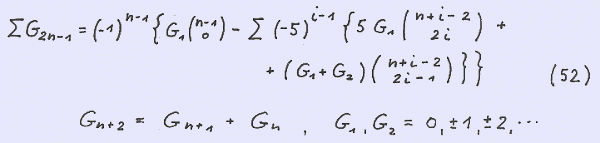
With the seeds S ( 1 , 2 ) and S ( 1 , 4 ) we obtain the formulae for the Fibonacci and the Lucas sequences:
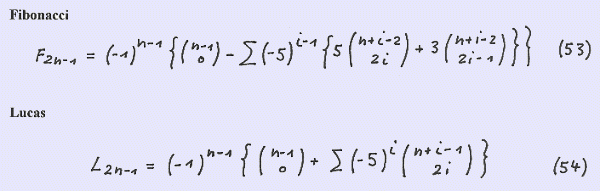
We give an example of the first five elements of the Fibonacci sequence:

4.
Another binomial summation formula for G ( 2n-1 ) reads
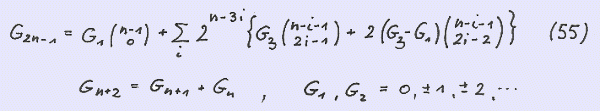
Again using the seed S ( 1, 2 ) yields F ( 2n-1 ) :
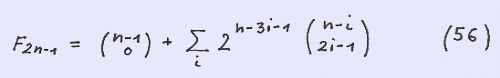
Below we give an example of the first nine elements of the sequence :

You are kindly invited to the next page where we will extend our binomial summation fomula
![]()
to the more general form