A Third Generalization (Part 1)



Welcome again to the wonderful world of Fibonacci mathematics. We will again derive formulae for rabbit populations others than the Fibonacci one. But before doing so let us start with the binomial summation formula for the generalised Fibonacci sequence G ( n ):
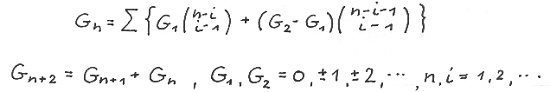
We consider now the sequence of every second element of G ( n ). There exist two sequences denoted by G (2n -1 ) and G ( 2n ) as illustrated up to n = 4 below:

The recurrence and binomial summation formulae for these two sequences read

We verify first the recurrence formulae and then show the binomial summation formulae fulfilling the recurrence formulae.
Observing G ( n ) = G ( n-1 ) + G ( n -2 ) and G ( n-1 ) = G ( n -2 ) + G ( n-3 )
we obtain G ( n ) = 2 G ( n -2 ) + G ( n-3 ) and with G ( n-3 ) = G ( n-2 ) - G (n-4 )
G ( n ) = 3 G ( n-2 ) - G ( n-4 ) . Replacing n by 2n+3 finally we obtain
G ( 2n+3 ) = 3 G ( 2n+1 ) - G ( 2n-1 ). Replacing n by 2n+4 we obtain
G ( 2n+4 ) = G ( 2n+2 ) - G ( 2n ).
For proof of the binomial summation expression for G ( 2n+3 ) we use
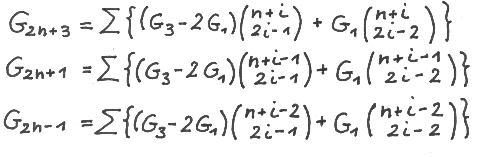
Rewriting G ( 2n+3 ) we obtain
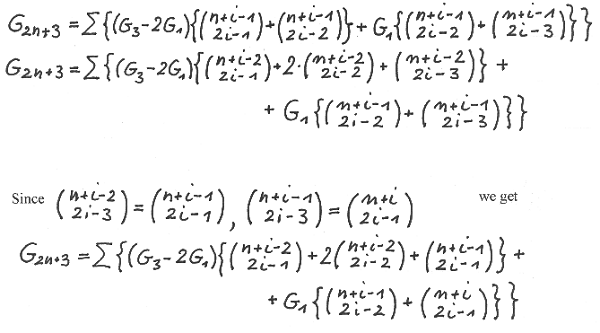
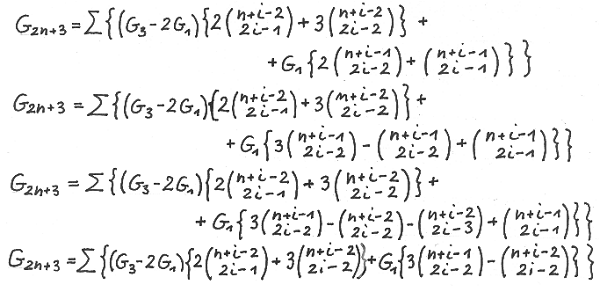
On the other hand we have
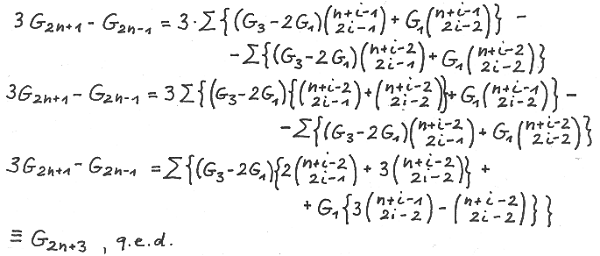
The proof for G ( 2n+4 ) is very similar to the one for G (2n+3 ).
Using G ( 1 ) = F ( 1 ) = 1 and G ( 3 ) = F ( 3 ) = 2 we obtain

Using G ( 2 ) = F ( 2 ) = 1 and G ( 4 ) = F ( 3 ) = 3 we obtain
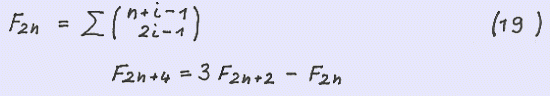
G ( 1 ) = L ( 1 ) = 1 , G ( 2 ) = L ( 2 ) = 3 , G ( 3 ) = L ( 3 ) = 4 and
G ( 4 ) = L ( 4 ) = 7 yields the Lucas sequence

We can replace n by 2n-1 and 2n respectively in our formula for G ( n ) yielding

and by comparison (16, 17)
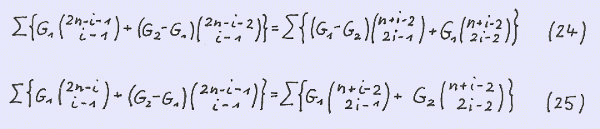
Using G ( 1 ) = G ( 2 ) = 1 we obtain
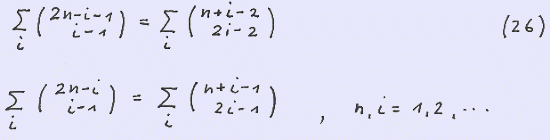
Summing up our formulae for G ( 2n-1 ) and G ( 2n ) over n observing ( 11 ) yields
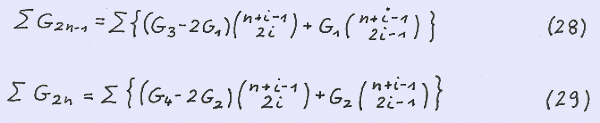
We rewrite ∑ G ( 2n-1 )
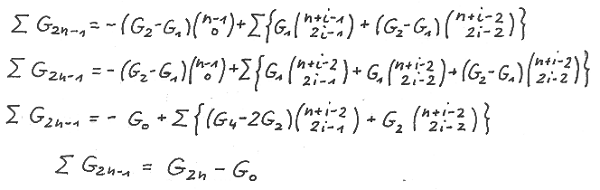
In a very similar way we can derive the formula for ∑ G ( 2n )
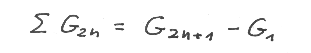
two very well known formulae ( 2 ).
Below we present an example of ∑ G ( 2n-1 ) with the seed ( 3 , -2 ) up to n = 5 :


Since at the beginning of this website we ask how we can determine the Fibonacci number for a given value of n without having to work all the terms of the preceding ones . We have an answer by our binomial summation formulae and with the respecticve Binet - formulae we have an additional possibility. These can be obtained by inserting into the respective Binet - formulae for G ( n ) the terms ( 2n-1 ) and ( 2n ) respectively yielding
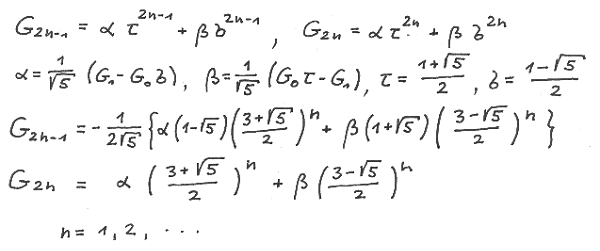
Observing

We obtain for the summation in formulae
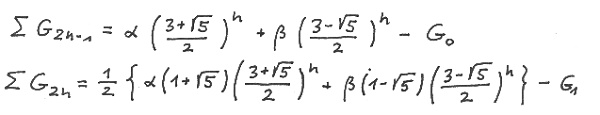
The world of Fibonacci binomial sums is more many-coloured than you might suggest from the above presentations. In the second part we give some examples of alternative representations indeed without proof since this will be done for more general formulae.