A Sixth Generalization

We continue in the following page with a binomial summation formula of the more general linear second order recurrence equation

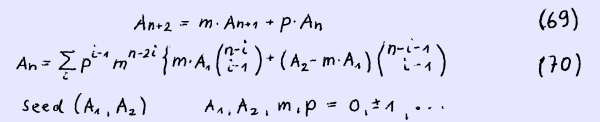
We proof by induction writing A_n in full yields

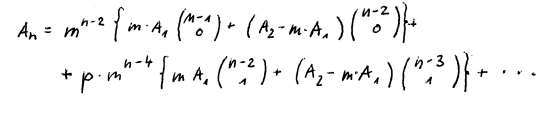
Obviously A₁ = m^-1 · m · A₁ is correct.

We assume A_n to be correct for n = r and n = r + 1 that is A_r and A_r+1.

Then we state A_r+2 = m A_r+1 + p A_r to be correct.

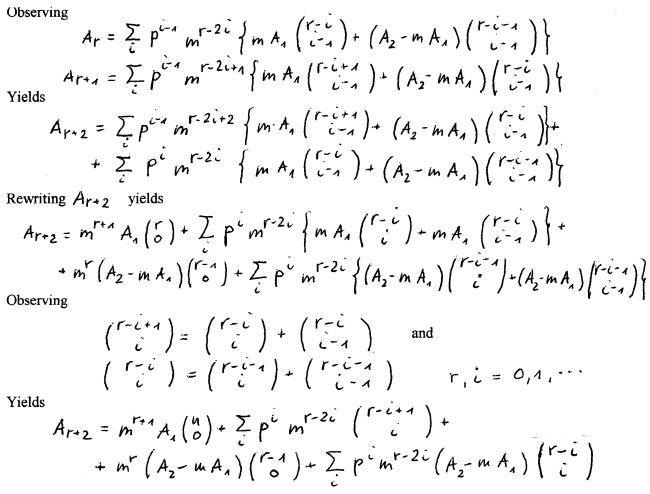
This is just our statement when replacing n by r + 2. So our binomial summation formula holds for any r.

From (70) some other formulae emerge. A linear second order recurrence formula in conjunction with a binomial summation formula for a serie composed of every k-th element of the generalized Fibonacci serie G_kn+e is given below.

We proof the recurrence formula by using Binets formula for G_k(n+1)+e and L_k obtaining

And by rearranging the above binomial summation formula we obtain finally

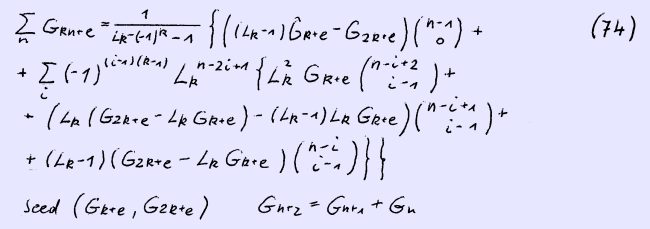
We consider now the more general case A_kn+e. Both the recurrence formula and the corresponding binomial summation formula are given below.

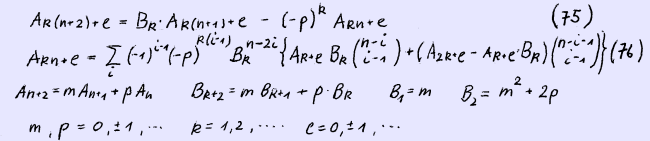
We proof first (75) in a very similar way then (71)

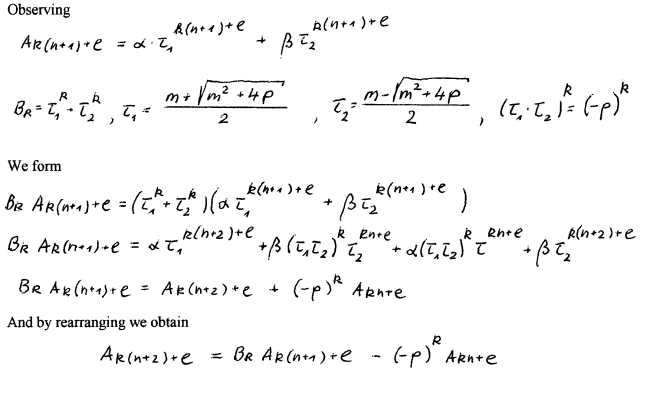
Observing (69) and (70) yields (76).

In particular when m = p = 1 we obtain formulae (71) and (72).

In our next page we are concerned with linear third order recurrence formulae, A recurrence formula

A_n+3 = A_n+2 + A_n+1 + A_n

has often been called a “Tribonacci“ sequence. We are concerned there with a sequence composed of the squares of F_n that is F²_n which leads to another linear third order recurrence formula. You are kindly invited to this page.