A Fifth Generalization

We derive some relationships of our recurrence formula

A ( n+2 ) = m · A ( n+1 ) - A ( n )

1. ∑ A ( n ) :

We rewrite the equation for A ( n ):

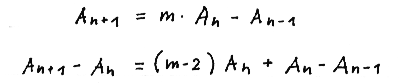
We sum up both sides of the equation over n yielding

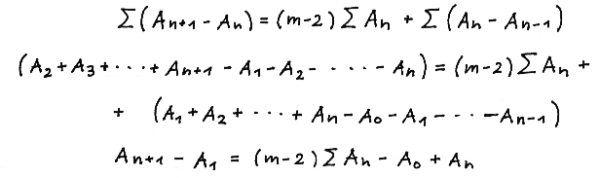
Observing A ( 2 ) = m · A ( 1 ) - A ( 0 ) finally yields

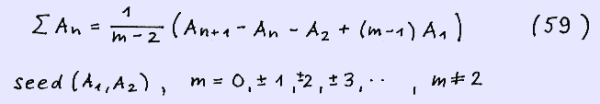
The binomial summation formula is achieved using equation (30)

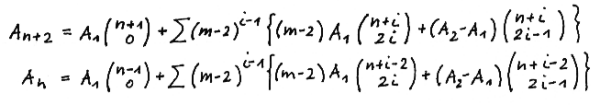
Writing equation (30) in full yields

Summing up over n yields

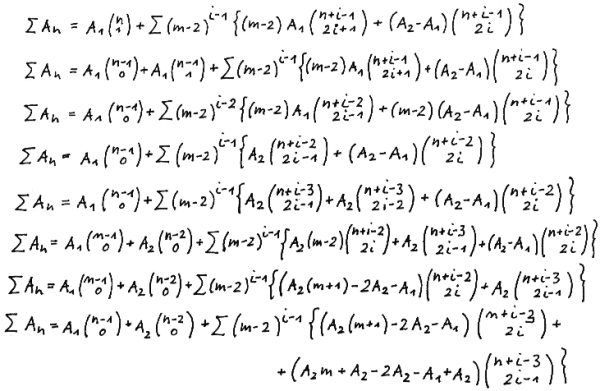
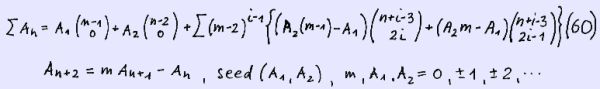
We give an example for n = 5:

m = 4 , A (1 ) = 1 , A ( 2 ) = 4

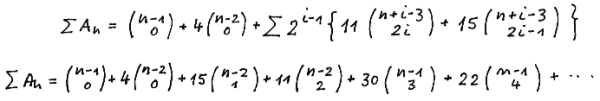
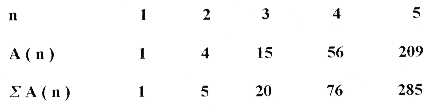
We present ∑ A ( n ) in the left - justified manner:

We ask now for a recurrence formula for ∑ A ( n ) and give the answer below and prove it later for a more general formula:

2. A ( 2n-1 ) , A ( 2n )

We start from equation A ( n ) = m · A ( n-1 ) - A ( n-2 ).

Observing

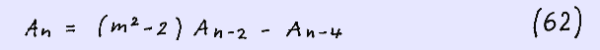
So we achieve a correlation between every second element of the sequence which is of the same form as the starting recurrence formula but m replaced by m² -2 and the seeds replaced in case of A ( 2n-1 ) by the seed ( A ( 1 ) , m · A ( 2 ) - A ( 1 ) ) , in case of A ( 2n ) by the seed ( A ( 2 ) , ( m - 1 ) A ( 2 ) - m A ( 1 ) ) yielding

3. ∑ A ( 2n-1 ) , ∑ A ( 2n ) :

We sum up both sides of the equations (63) and (64) over n and obtain

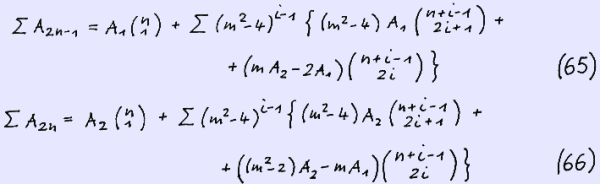
We give an example for ∑ A ( 2n ) , m = -3 , seed ( - 2 , 1 ) and n = 5.

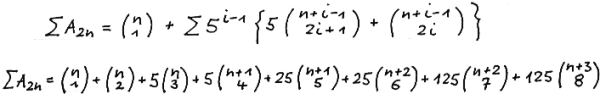
We present ∑ A ( 2n ) in the left justified manner.

We can derive formulae for ∑ A ( 2n ) and ∑ A ( 2n-1 ) equivalent to equation ( 59 ) rewriting equation ( 62).

Observing A ( 2 ) = m · A ( 1 ) - A ( 0 ) yields

In a very similar way we can obtain

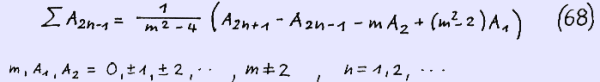
In our next page we will present binomial summation formulae for the more general recurrence formula A ( n+2 ) = m · A ( n+1 ) + p · A ( n ) and G ( k n + l ) . You are kindly invited to visit this page.