A Fourth Generalization

In our last page we presented a binomial summation formula of a sequence composed of every second element of the generalized Fibonacci sequence obeying the recurrence formula

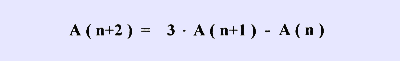
In this page we present the binomial summation formula of the more general recurrence formula

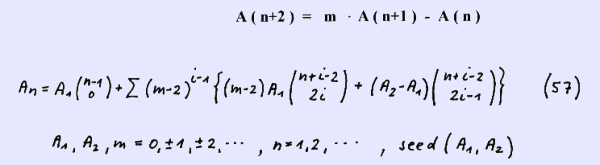
We verify this binomial summation formula by showing that it fulfils the above recurrence formula.

Rewriting the recurrence formula yields

A ( n+2 ) = ( m-2 ) · A ( n+1 ) + 2 · A ( n+1 ) - A ( n )

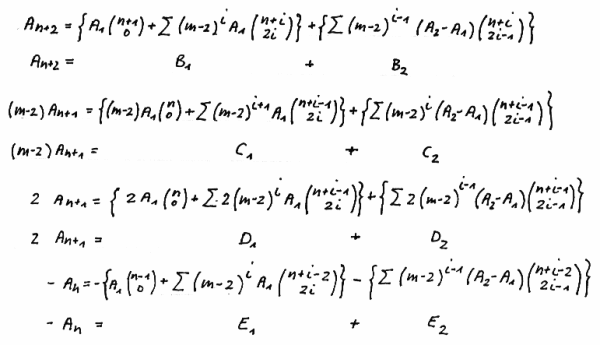
We prove the sums S(1) = B(1) + C(1) + D(1) + E(1) and
S(2) = B(2) + C(2) + D(2) + E(2) separately. Obviously it is then verified for the sum S = S(1) + S(2).

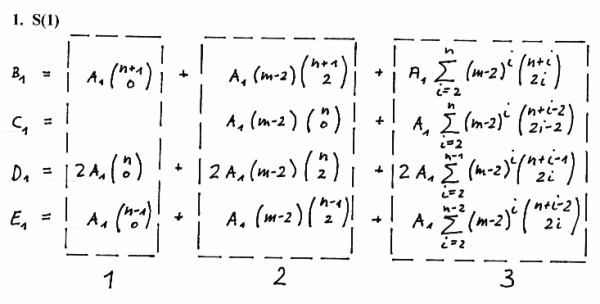
Proving 1 yields

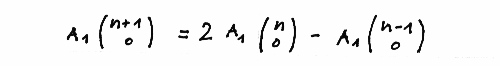
Proving 2 yields

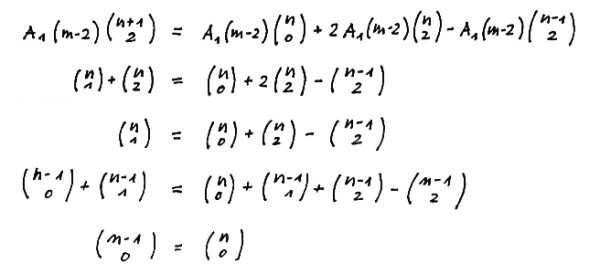
Proving 3 yields

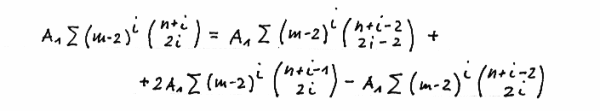
Observing

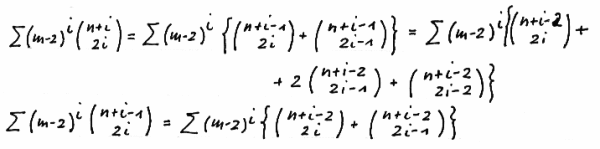
yields

In a very similar way we can prove S(2)

Below we give three examples for m = 0 , m = 1 and m = 2. As we know from our previous pages the case m = 3 yields with the seed ( 1 , 2 ) the sequence of every second element of the Fibonacci sequence, i.e. F ( 2n - 1 ), n = 1 , 2 , · · · .

m = 0 , seed ( 1 , 2 ) :

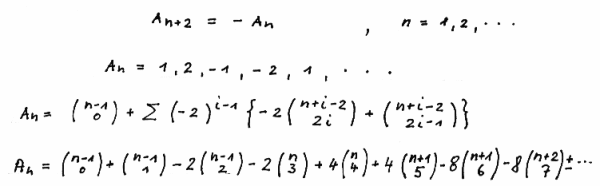
We show in the left-justified manner of the Pascal Triangle the contribution of the binomial coefficients to the elements of the sequence up to n =5.

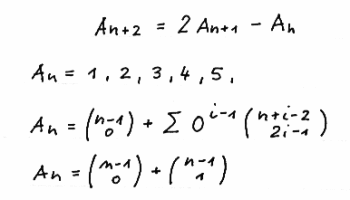
We give here another binomial sum presentation of the recurrence formula
A(n+2) = m · A(n+1) - A(n) without proof which will be done in a later page for a more general formula.

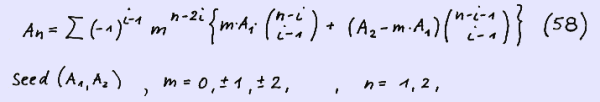
As an example we show the case m = 3 with the seed = ( 1 , 2 ) yielding our well known sequence for F ( 2n-1 ) :

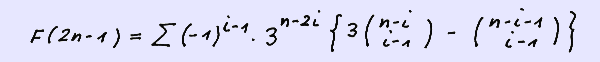
Below we show the contribution of the formula to the first five elements of the sequence:

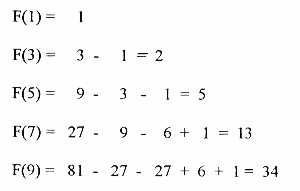
In our next page we will derive some formulae and relationships of the recurrence equation presented above: A(n+2) = m · A(n+1) - A(n). You are kindly invited to this page.