A Second Generalization

On this page we present binomial summation formulae for the generalised Fibonacci sequence G(n) and the sum ∑ G(n) of its first n elements. You are now familiar with the binomial presentation

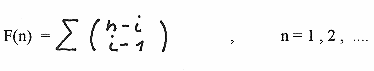
( see formula (1) in the first generalization )

written down in full

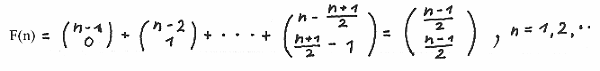
which is the Fibonacci sequence moved one position to the left , since the summation starts with n = 1.
(n-1)/2 is defining the largest integer.

The sequence is defined by a seed (1,1) and a recurrence formula F(n+2) = F(n+1) + F(n). The sequence can be expanded to negativ values of n as shown below:

We ask now how will the binomial presentation looks like if we start the Fibonacci sequence with any two consecutive Fibonacci numbers , say seed (5,-3).

To answer this question we look for a binomial presentation of a sequence which starts with a seed of any two numbers S ( G(1) , G(2) ) and which follows a recurrence formula G(n+2) = G(n+1) + G(n). This is called a generalised Fibonacci sequence .

Its binomial summation formula is

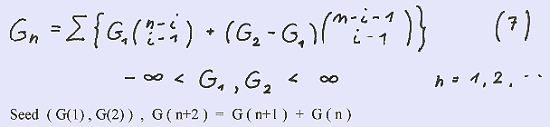
We proof this summation formula by showing that it fullfills the recurrence formula

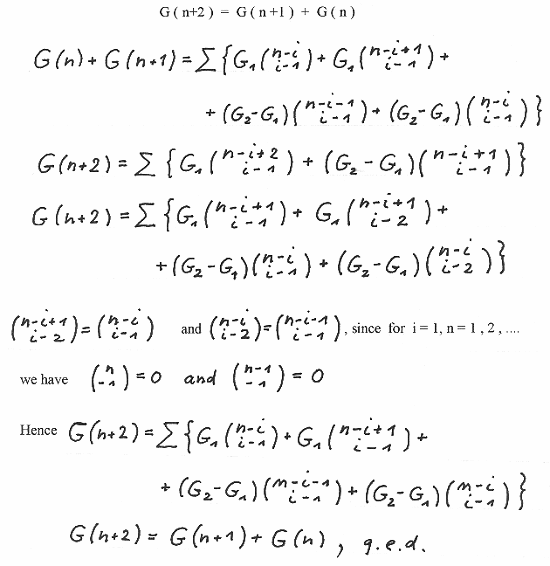
Now using the seed S ( F(k) , F(k+1) ) we have

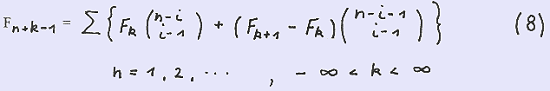
As an example we use as mentioned above the seed S (5,-3) , k = -5 and obtain

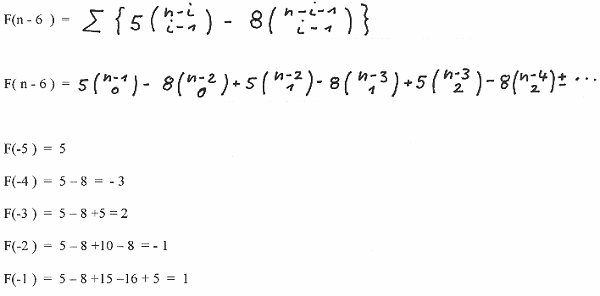
and so forth.

Another well known sequence is the Lucas - sequence :

defined by the seed S ( 2 , 1 ) and the recurrence formula L( n+2 ) = L(n+1 ) + L(n). Since we start our binomial presentation with n = 1 we use the seed S (1 , 3 ). By applying our general formula for G(n) we obtain

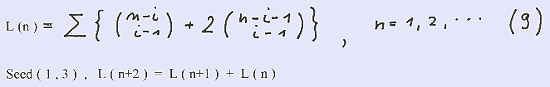
Finally we present below the binomial presentation of the sum of the first n numbers of the sequence G(n):

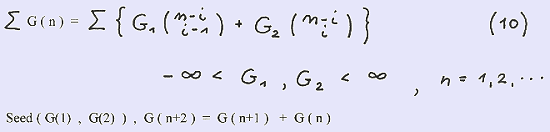
We proof this formula by writing down in full G (n) and summing up both sides over n :

We make use of the relation

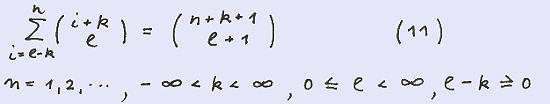
and obtain

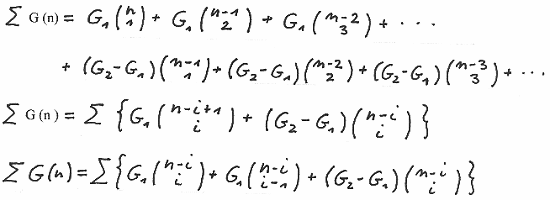
and finally

We rewrite the equation from above

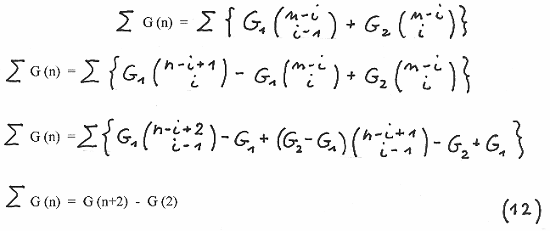
a well known formula for the sum of the first n elements of G (n)

Rewriting

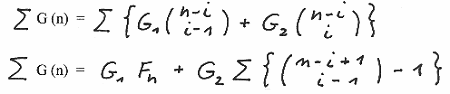
we obtain

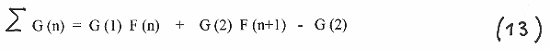
With S (1 , 1 ) and S ( 1 , 3 ) we obtain the sums for the Fibonacci - and Lucas sequences:

As an example we show below the sum ∑ G (n) with a seed ( - 2 , 3 ) up to n = 6 :

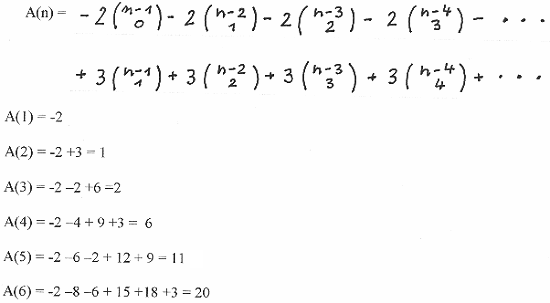
We finish this page now and will continue in our 3 rd generalization with the presentation of binomial formulae for G (2n ) , G (2n-1) , ∑ G ( 2n ) and ∑ G ( 2n-1 ). You are kindly invited to this page.